
“Cómo es posible que la matemática, un producto del pensamiento humano independiente de la experiencia, se adapte tan admirablemente a los objetos de la realidad”
Puede bajar los siguientes archivos que complementan la explicación:
La solución común para generar un código datamatrix en un centro de maquinado es comprar una macro (SW tiene una muy buena pero solo jala en sinumerik) o hacerlo después del maquinado. Pero en ocasiones puede ser mejor tener un programa CNC que pueda grabar un código en la pieza. Un código datamatrix codifica una cadena de caracteres en un símbolo. El símbolo está formado por un conjunto de módulos, cada módulo representa un bit, un módulo "lleno" representa un 1, mientras que uno vacío es 0.
El símbolo está limitado por dos líneas que forman una "L" que sirven para alinear el código. En el lado opuesto está formado por dos líneas de modulos llenos y vacíos colocados de forma alternada, este lado determina el tamaño del módulo.

La cadena de caracteres que se desea codificar se convierten en "claves", cada clave tiene una longitud de 8 bits. La ventaja del código datamatrix es su redundancia o paridad, ya que se agregán claves que permiten que la cadena de caracteres pueda ser recuperada a pesar de que el símbolo esté incompleto o no escanee apropiadamente. Este proceso de corrección de errores se logra mediante el algoritmo de “Reed Solomón”
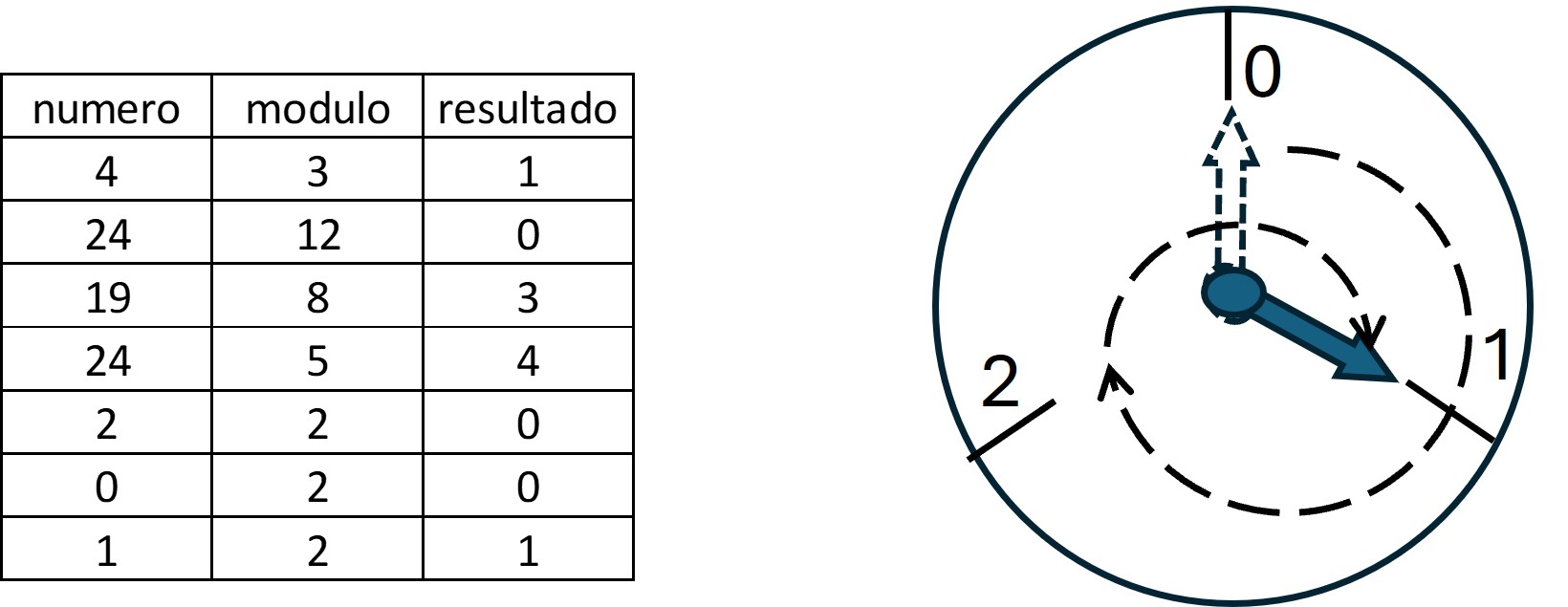
El algoritmo de Reed Solomon se basa en el algebra de “campos de Galois”. El entender el algebra de campos es la parte más díficil para un ingeniero de manufactura, pero para su implementación no se requiere un conocimiento tan profundo (aunque sería deseable). El algebra de campos finitos no es igual al algebra común, la cuál opera en un campo infinito de números. El algebra de campos finitos se basa en un campo con un número limitado de elementos. Por ejemplo si se tienen un "campo" de solo dos elementos, el 0 y el 1, la suma de 0+1 es igual a 1, como en el algebra que todos conocemos. En el algebra "común" la suma de 1+1=2, peros será igual a 1 en el algebra de campos finitos (para un campo de dos elementos). Por ejemplo, suponga que tiene un campo de 12 elementos(0,1,2,3,4,5,6,7,8,9,10,11), como en un reloj. si suma 12 +12 el resultado sería 24 para el algebra "común", pero será cero en el campo finito. La explicación del reloj nos indica que el resultado sería el residuo de la operación, esto se puede expresar como una operación "modulo" (que se puede realizar en ms excel). La analogía del reloj puede servir cuando queremos expresar un número en un campo de elementos finitos. Por ejemplo, el número 4 en un campo de tres elementos (0,1,2) sería igual a 1, que también se puede expresar como 4 mod 1. En la figura se muestra como un reloj de tres elementos (0,1,2) expresaría el número 4. Los primeros tres elementos completarian una vuelta a los tres elementos y solo quedaría el residuo.
.
A rasgos muy generales la idea tras el algoritmo de Reed Solomón es que de acuerdo a la teoría de campos de Galois, si tenemos un campo de n elementos podemos reconstruir todo el campo si conocemos el valor de un polinomio de menor grado. La explicación es más profunda pero para nuestros propósitos es suficiente. Así, podemos codificar la cadena de caracteres como un polinomio de grado N que a su vez es dividido por un polinomio conocido. Con el residuo de la division se pueden construir los valores de corrección de error. Todas estas operaciones se daran dentro de un campo de 256 elementos (0,1,...255).
La cantidad de claves de datos que se pueden guardar en un símbolo está determinada por el número de filas y columnas. Es importante aclarar que la cantidad de "claves" no es necesariamente igual a la cantidad de caracteres que queremos codificar, ya que hay modos en los que se pueden agrupar más de un caracter en una clave
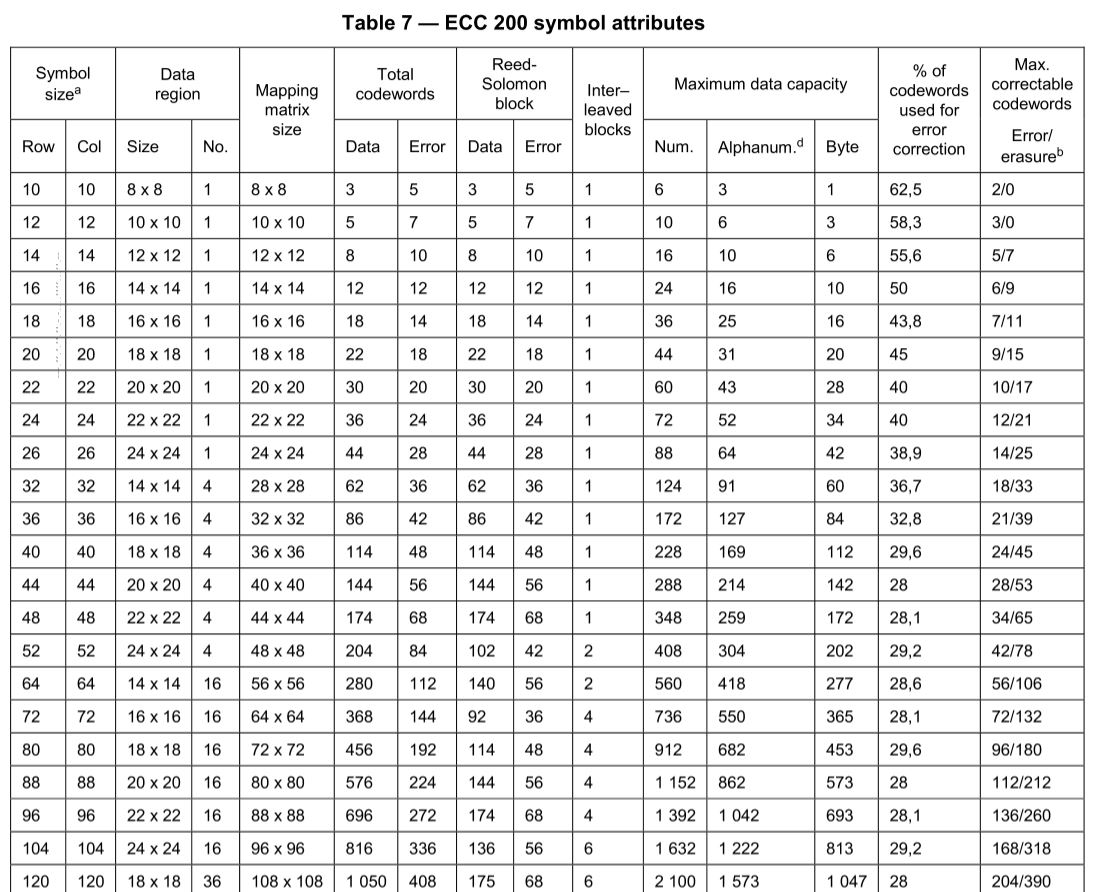
Existen diversos modos de codificación, siendo el modo ASCII el que se usa por defecto. Los otros tienen ciertas ventajas como la de poder codificar más caracteres en una sola clave, aunque están más limitados en los caracteres que pueden codficar. En la tabla anexa se muestra como el modo ASCII puede requerir hasta 16 bits para codificar un caracter, pero el modo C40 solo requiere 5, con la desventaja de que el modo C40 está limitado a menos caracteres. Cada modo tiene reglas distintas para codificar los caracteres.
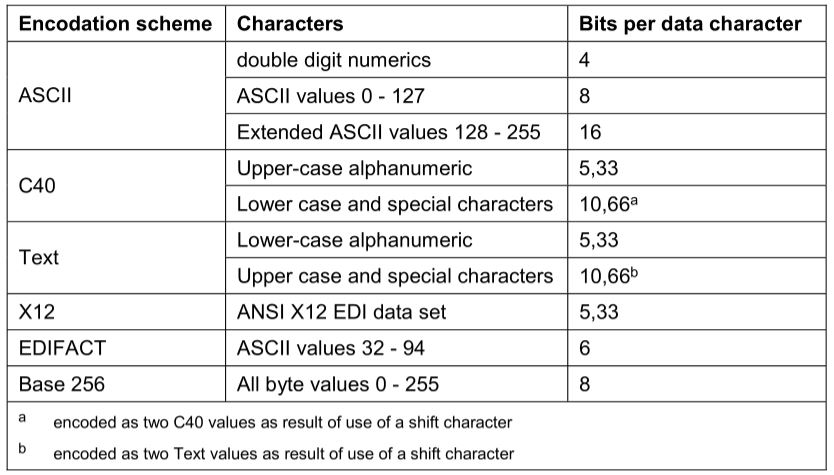
Los pasos para codificar una cadena de caracteres sería la siguiente
Se codificará la frase "ANITA LAVA LA TINA" en modo ASCII. La cantidad de caracteres es de 18, por lo que elegiremos un símbolo de 18 filas, que puede almacenar hasta 22 claves de datos y 18 claves de corrección de error. La figura 5 muestra la ubicación de cada bit de las claves.

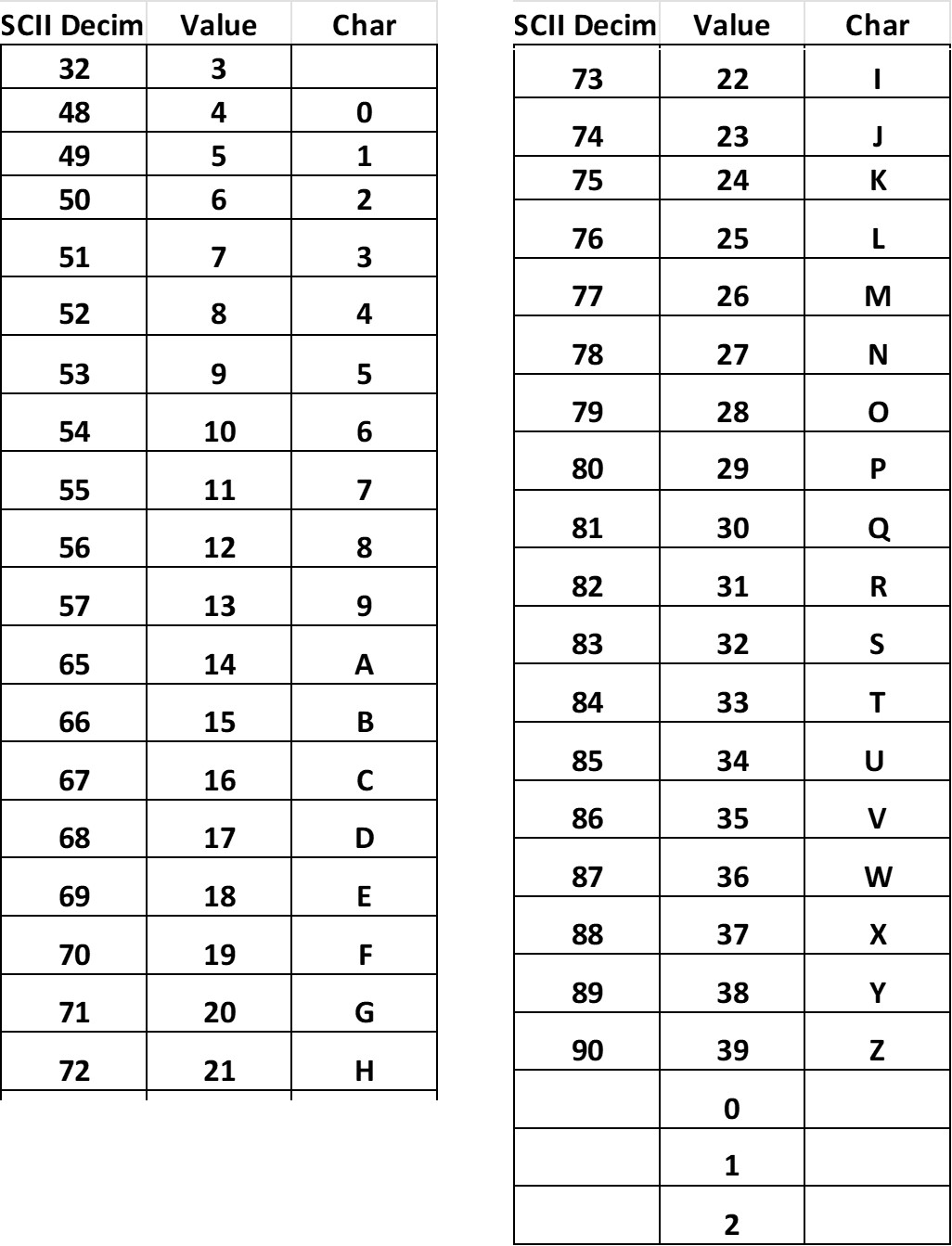
La codificación siempre se basa en el valor decimal del caracter de acuerdo a la tabla ASCII (figura 6 y 7). y sigue las siguientes reglas
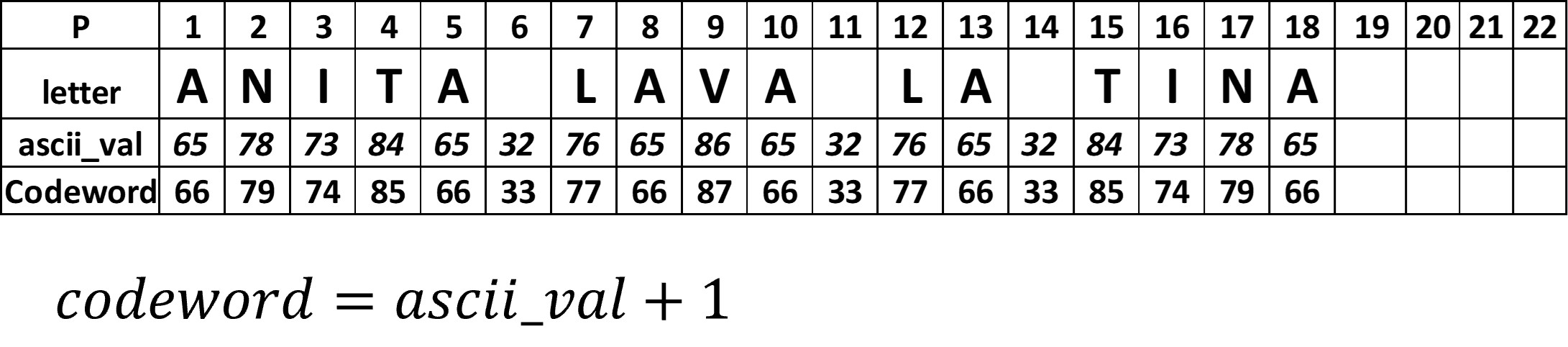
Un símbolo de 18 filas puede guardar 22 claves de datos, pero la cadena de caracteres solo tiene 18. Cuando existen claves sobrantes se tendrán que llenar usando las siguientes reglas:
La figura 8 muestra las claves completas para los datos, como únicamente es texto a cada caracter le corresponde una clave, se agregan además 4 claves para espacios vacios.
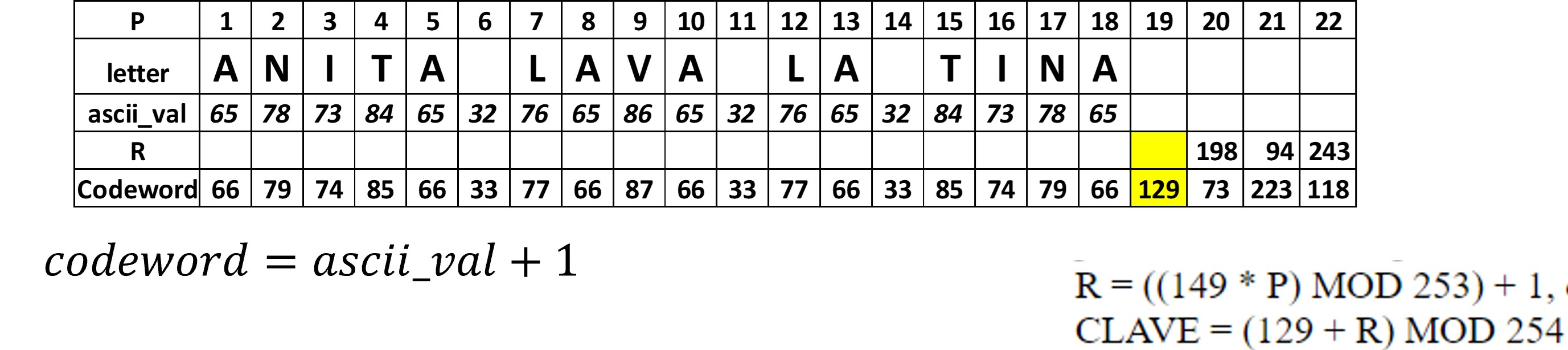
Las claves encontradas se usaran como los coeficientes del polinomio de datos en el algoritmo de Reed Solomon. De manera muy general el objetivo es construir un polinomio final c(x). De acuerdo a la formula de la figura 9.

El grado del polinomio de datos se establece en función de la cantidad de claves de datos k, en este caso la cantidad de claves es k=22, el grado sera k-1=21 ya que el valor de las potencias empieza en cero (0,1,...21). Este polinomio se multiplica por x elevada a n-k. El propósito de esta operación es dejar espacio para los polinomios de control.

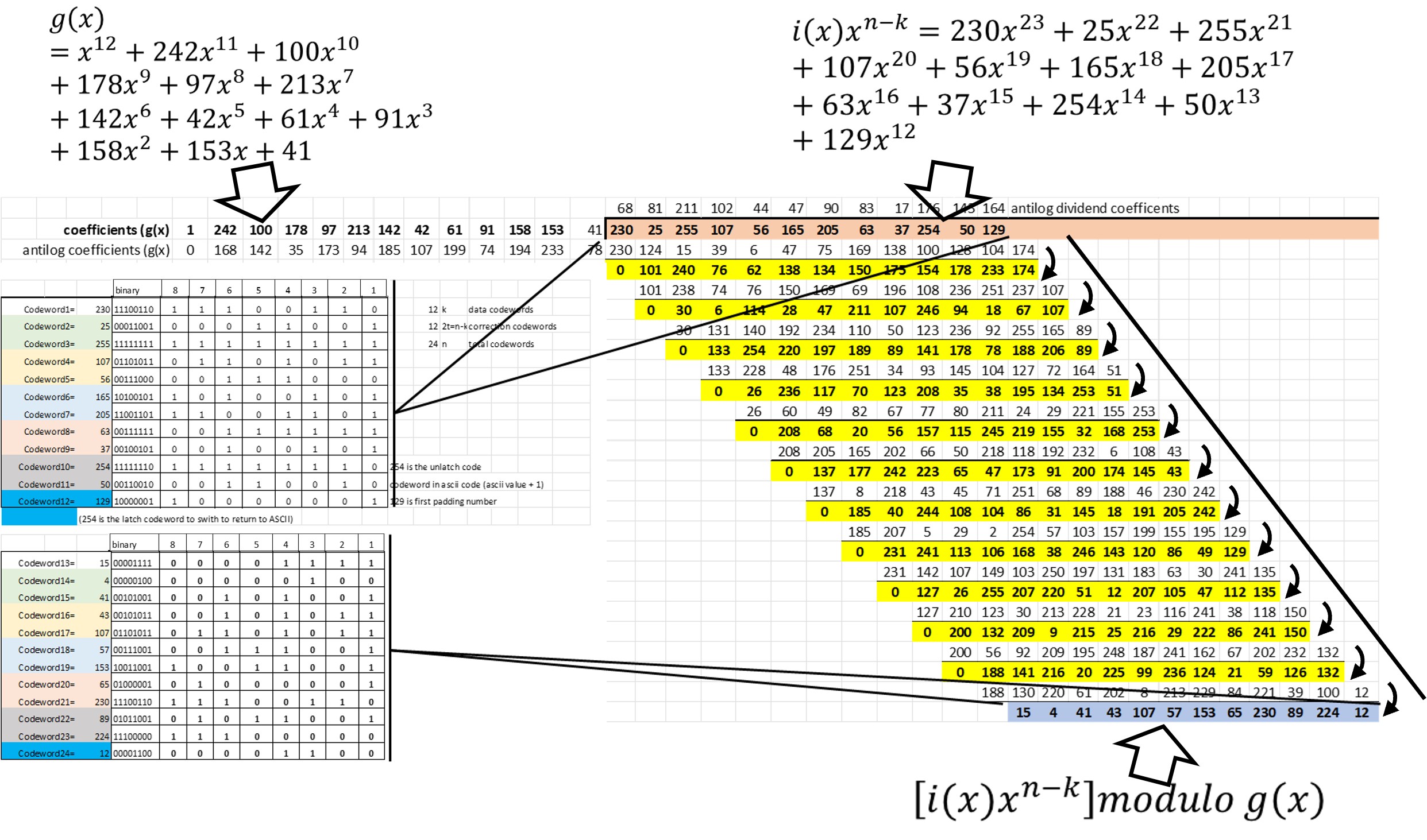
En la figura 10 se muestra la primera parte que compone el polinomio final c(x) El polinomio de control es una operación módulo, es decir el residuo de la division del polinomio i(x)x^(n-k) entre el polinomio generador g(x). El polinomio g(x) se puede calcular usando el algoritmo del estándar, sin embargo el estándar también los proporciona desarrollados de acuerdo a la cantidad de claves de corrección de datos. Para nuestro ejemplo con 18 claves de corrección de error el polinomio se muestra en la figura 11. En la figura 12 se muestra una visualización de la operación módulo, en ella se muestra que el resultado sería el residuo de la división del polinomio de datos entre el polinomio generador,
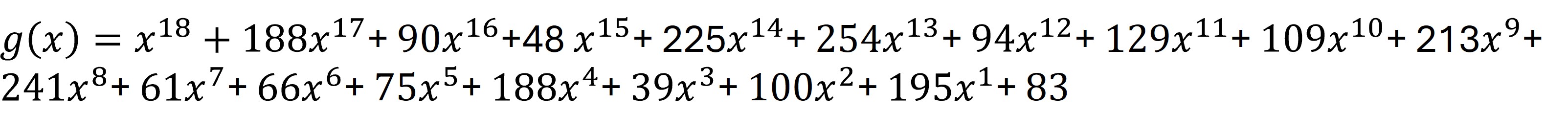
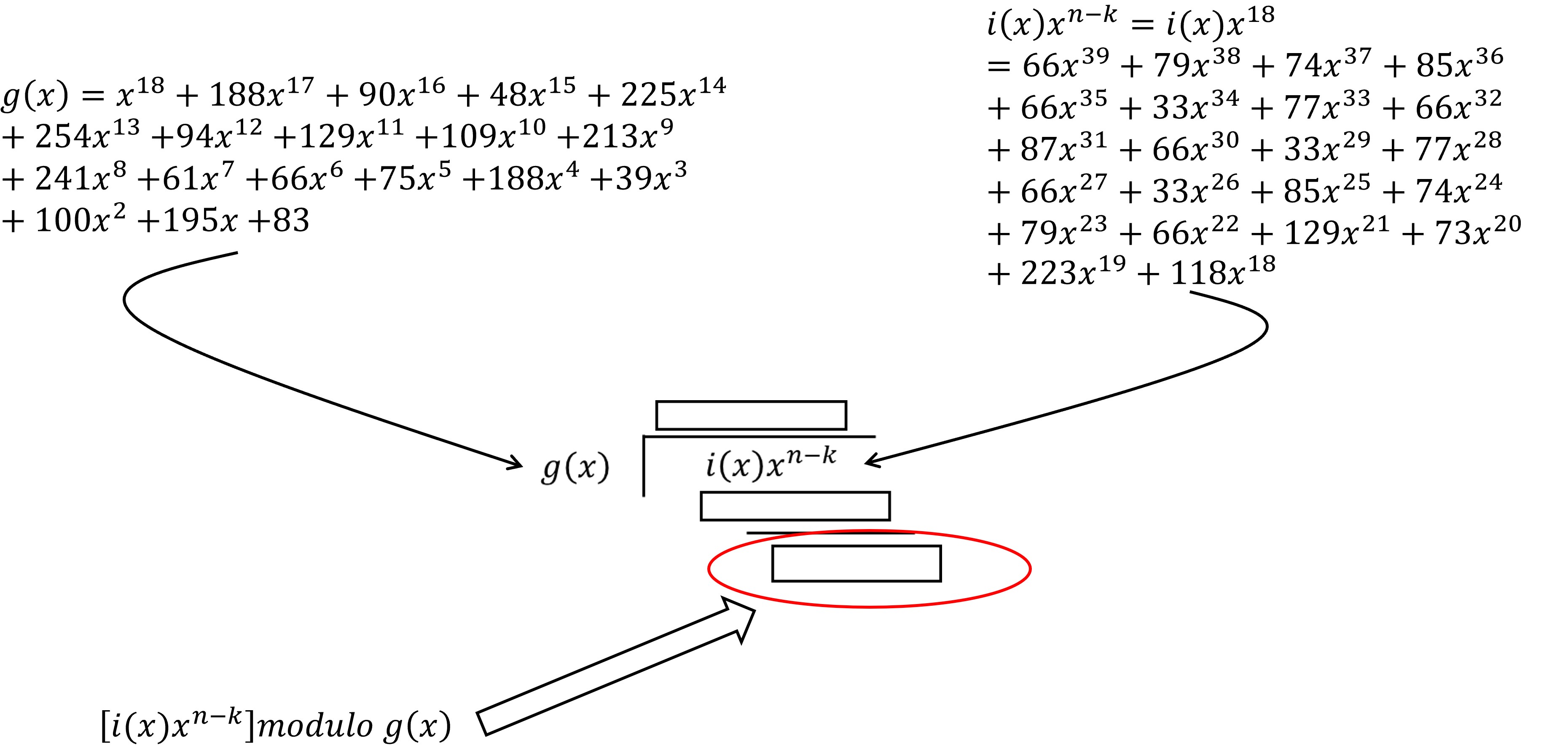
La división de polinomios se debe realizar en el campo finito de 256. Para realizarlo de manera más sencilla se hace uso de tablas de logaritmos especiales para ese campo.
El proceso consiste en obtener los antilogaritmos (de campo finito 256) de los coeficientes del dividendo y del divisor. El proceso es repetitivo para cada uno de los coeficientes del dividendo. En cada etapa el antilogaritmo del coeficiente del dividendo se suma al antilogaritmo de cada coeficiente del divisor, esa suma es modulo 255, y para ese resultado se obtiene el logaritmo. Cuando se completa la secuencia para cada coeficiente del divisor se realiza una operación XOR para obtener el resultado y se repite el proceso.
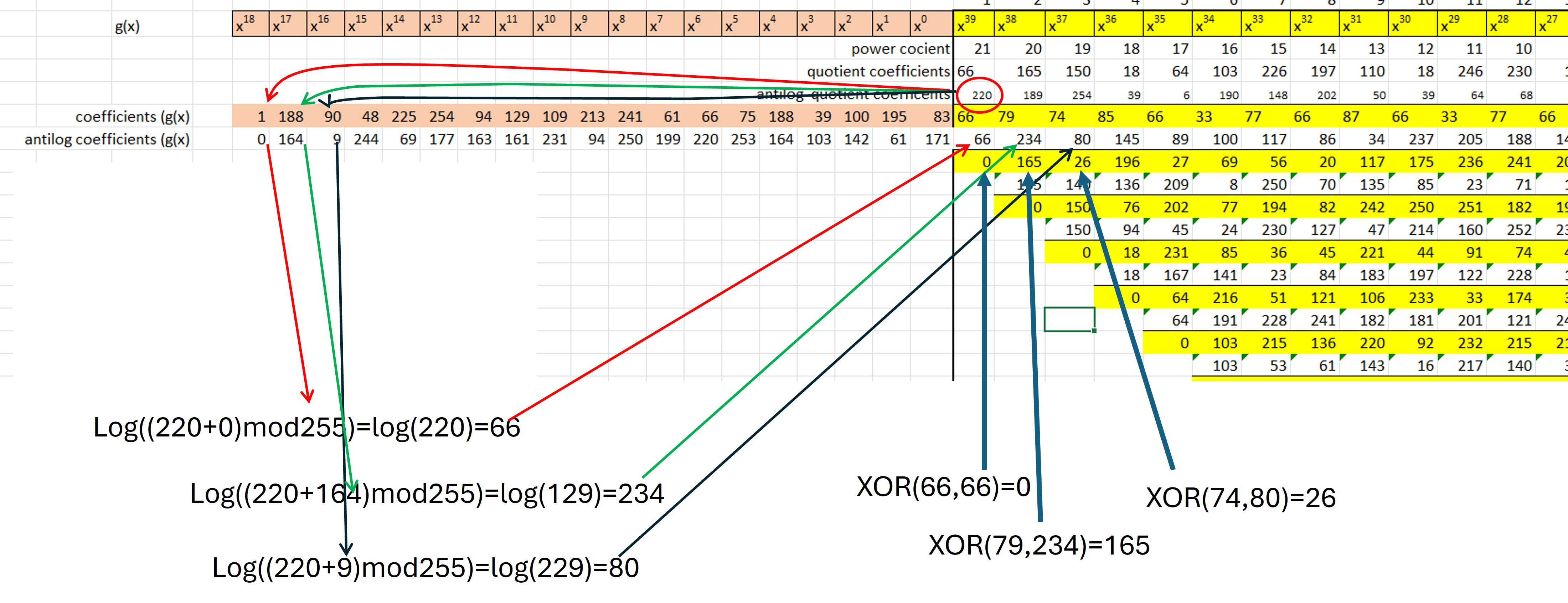
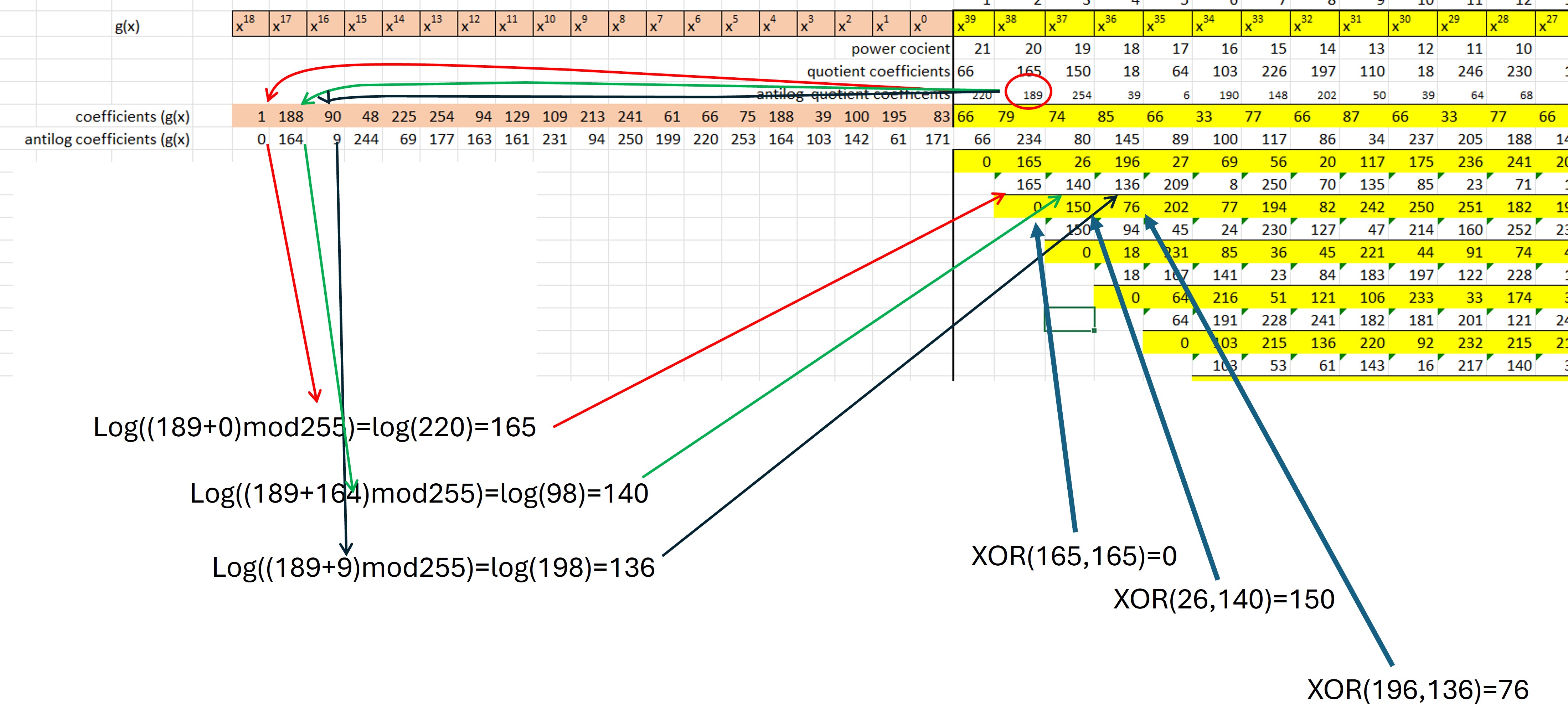
Al completar las operaciones para todos los coeficientes del dividendo se obtendrá un residuo, el cuál es el módulo. Los valores del residuo son los coeficientes del polinomio de control (Figura 9). Los coeficientes del polinomio de datos se muestran en amarillo en la figura 16, y en azul los coeficientes del polinomio de control.

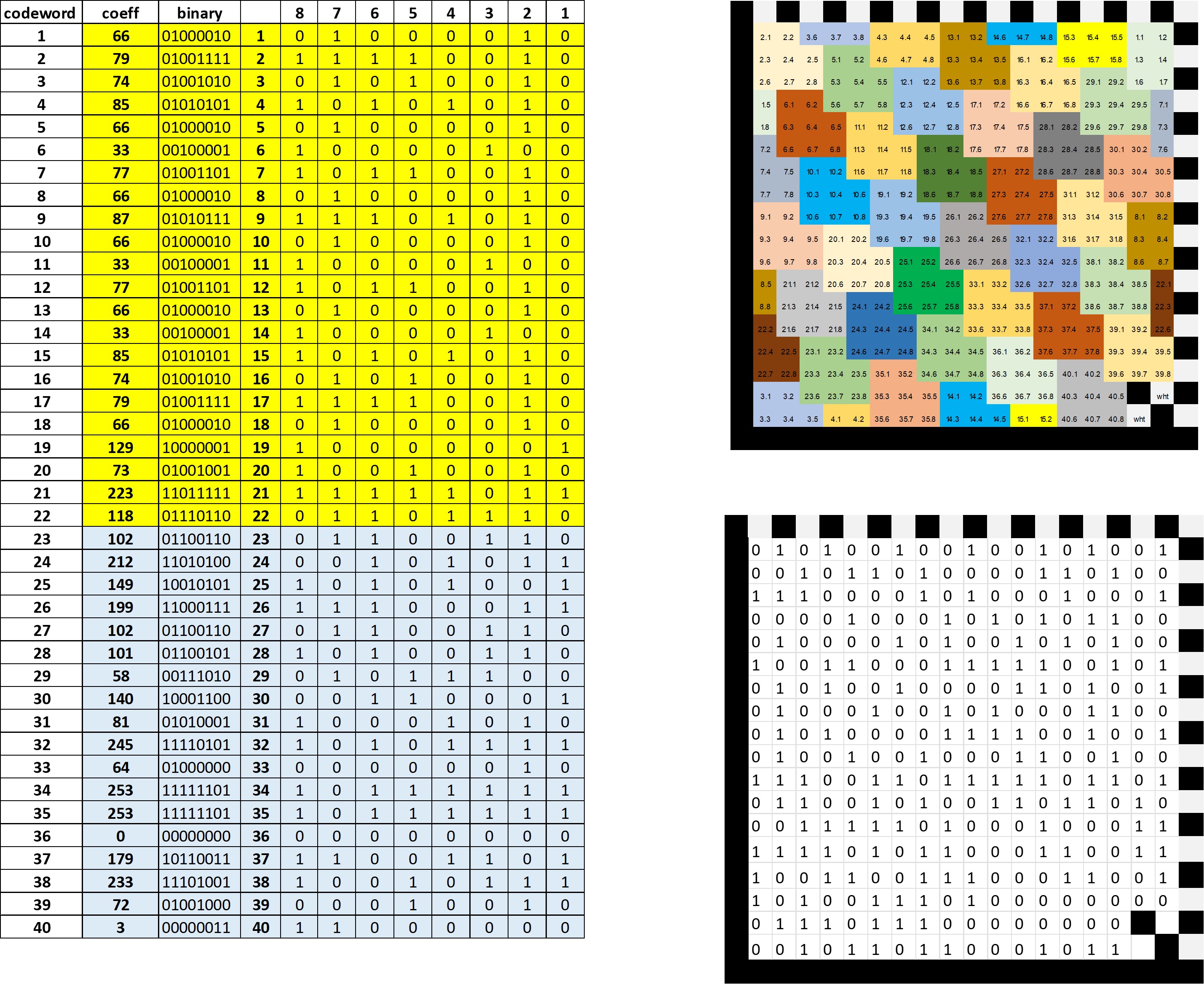
Cada clave obtenida del proceso anterior debe ser expresada en forma de 8 bits. Cada uno de los valores del bit individual se acomodan de acuerdo al mapeo del símbolo de la figura 5. Al final los valores de 1 se expresan como un modelo lleno y los ceros con un modulo vacío, el proceso está completo (Figura 17).

Vamos a codificar un número de serie que consiste de 13 caracteres alfanúmericos ("02AD23MH06001"), formado únicamente por mayúsculas y números. Cómo es una operación de maquinado nos interesa usar la menor cantidad de caracteres, así que en lugar del modo ASCII usaremos el modo C40. Este modo permite agrupar 3 caracteres en dos claves, lo que permite ahorrar espacio y tiempo.
En cuanto al símbolo, el más adecuado para nuestros propósitos es uno de 16 X 16, que es capaz de almacenar 12 claves de datos y 12 de corrección de errores.
En el modo C40 cada caracter tiene un valor decimal, cada 3 caracteres consecutivos (C1, C2, C3) se codifican con la formula (1600*C1)+(40*C2)+C3+1.
Esta fórmula puede generar un valor de 1 a 64000
Posteriormente se obtienen dos claves:
Como el modo predeterminado es ASCII, debemos indicar que se cambia a modo C40 usando la clave 230 (latch code) antes de las claves de datos. Si se requiere volver al modo ASCII se coloca la clave 254 (a codificación en modo ASCII es igual al valor decimal más uno).
La figura 18 muestra el cálculo de los valore de 16 bits para los primeros tres caracteres. Cada caracter tiene un valor de acuerdo al valor de la tabla para el código C40.

Al calcular el valor de 16 bits vemos que solo hay suficientes caracteres para completar 4 valores de 16 bits. De cada uno de esos valores se obtienen dos claves, es decir, tenemos 8 claves. La primera clave de los datos debe ser el valor 230 para indicar que estamos cambiando a modo C40, posteriormente poner las claves de datos, que son 8 en este caso, por lo que tenemos 9 claves de 12 disponibles. Vemos que aún tenemos que codificar un caracter, que por simplicidad codificariamos en ASCII, por lo que la décima clave será el valor 254 para regresar a ese modo. La onceava clave sería el valor del caracter en modo ASCII (valor decimal + 1), y la doceava clave sería un valor de "padding".
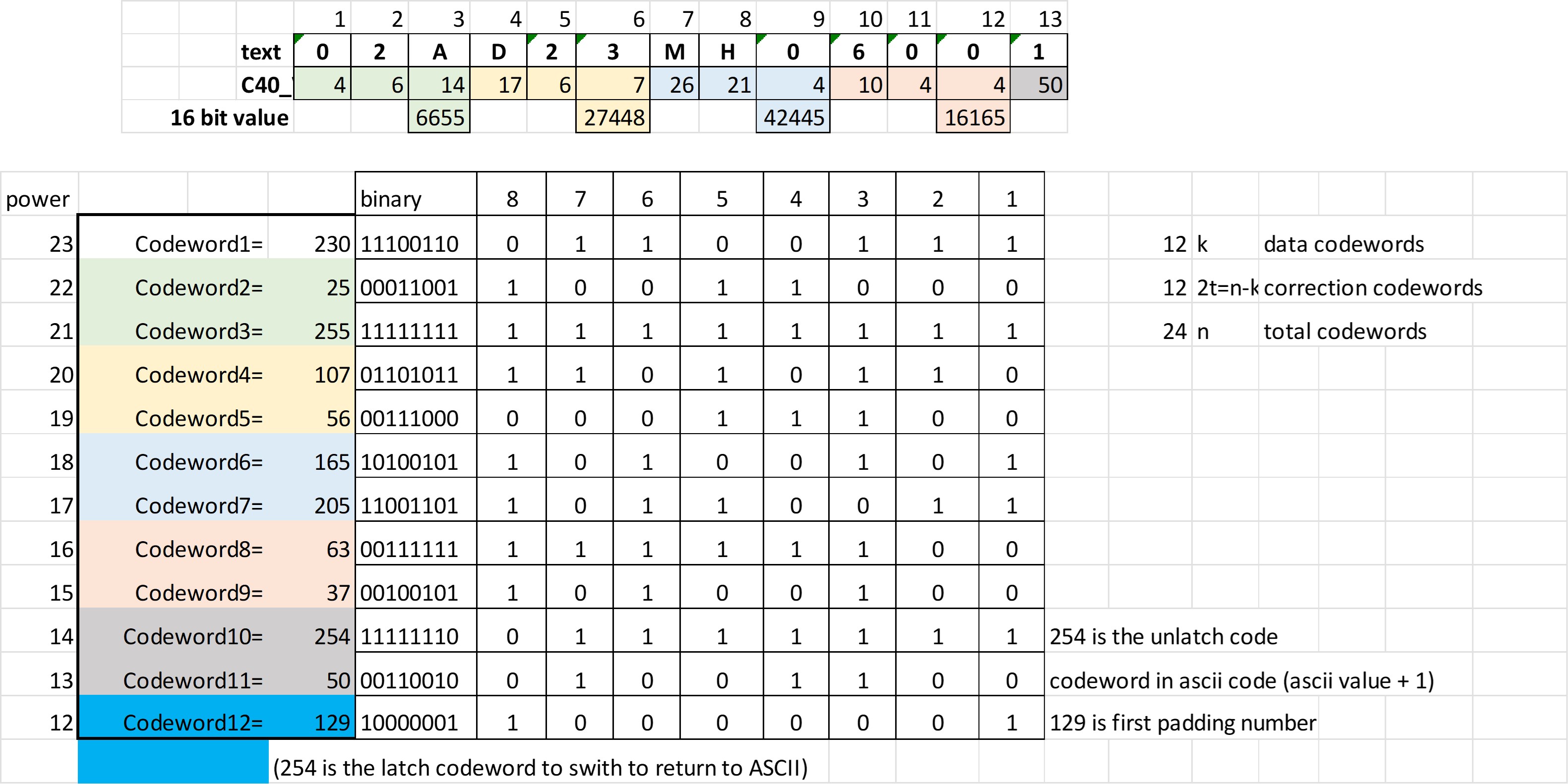
Las claves de corrección de errores serían también 12 y se obtienen como se mostró anteriormente: de la división del polinomio expandido usando como coeficientes del dividendo las claves de datos obtenidas previamente. Los valores del polinomio g(x) del divisor se obtienen del estándar.
El proceso de división debe realizarse de manera recursiva hasta obtener el residuo, es decir su módulo.Cada etapa tiene que usar los antilogaritmos (base 256) realizando una operación XOR.
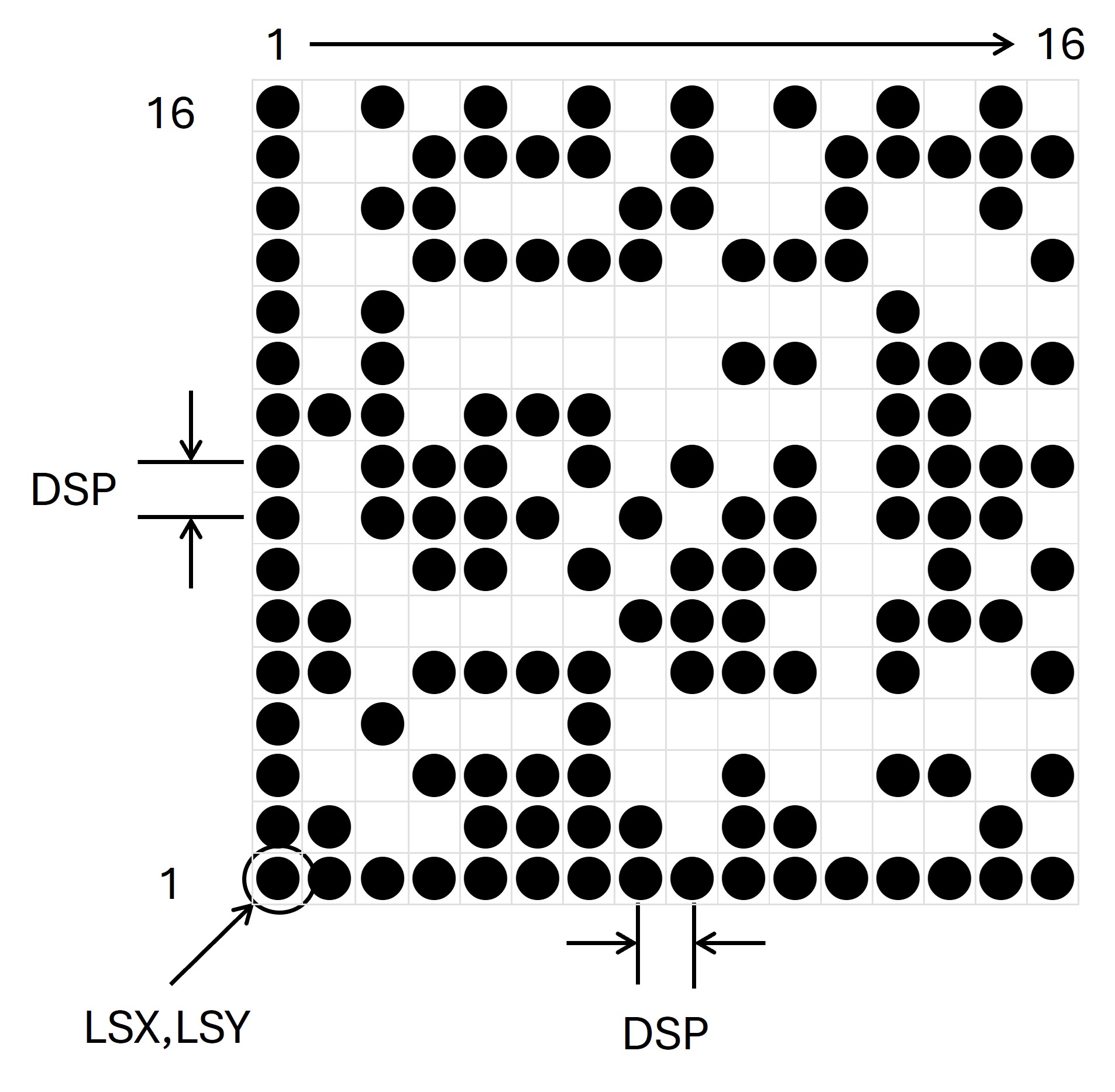
Para crear un programa en CNC solo se requiere convertir cada modulo del símbolo en una coordenada y programar un marcaje si el modulo es 1 y omitirla si es 0.
Los bordes del símbolo ya tienen definidos sus valores, por lo que su programación es sencilla. Al dividir todo el símbolo en columnas solo requerimos determinar el valor individual de cada punto. Identificaremos la posición de la esquina inferior izquierdo por las coordeadas (LSX, LSY), la sepración entre puntos será el valor de la variable DSP.
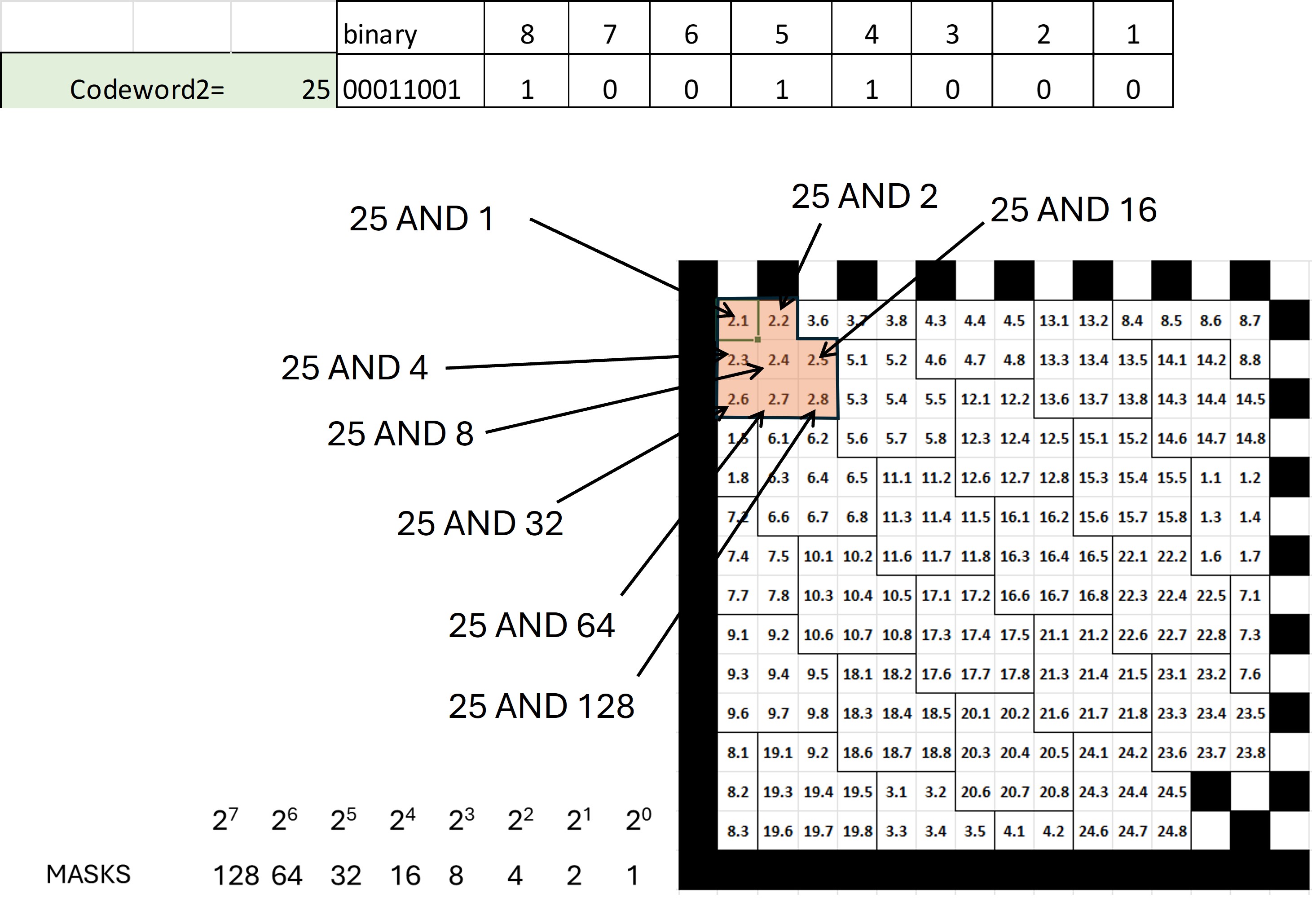
Cada clave consiste de 8 bits y cada bit tiene una ubicación predifinida en símbolo. En la figura 21 se muestra como el valor de la clave 2 tiene un valor de 25 cuyos bits son 00011001
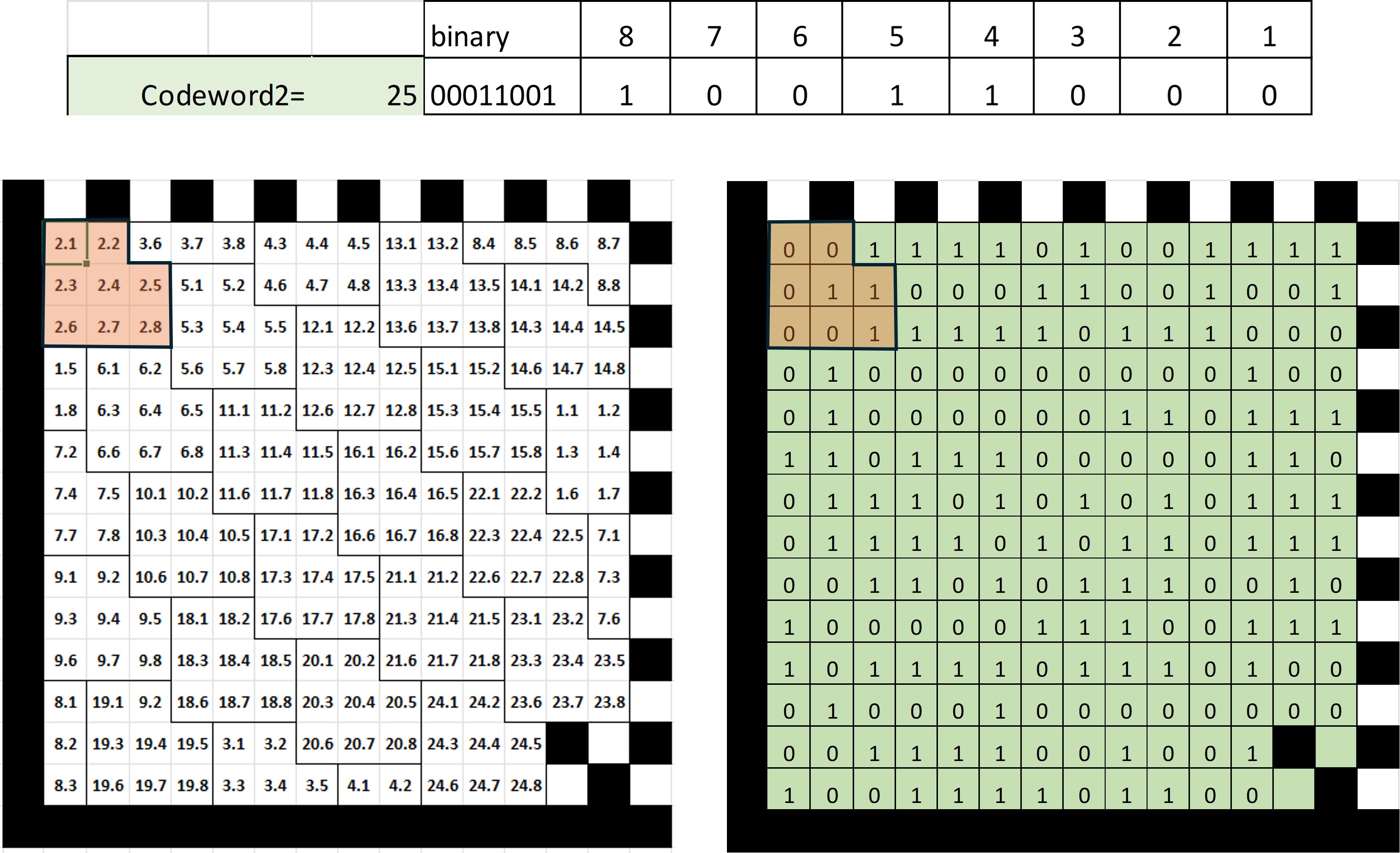
Cuando se programa el marcaje se debe aislar el valor de cada bit de acuerdo a su posición en el símbolo. La manera de lograrlo es por medio de una "máscara" con una operación AND con un valor binario que solo tenga el valor "1" en la mismpa posición del bit de interés.
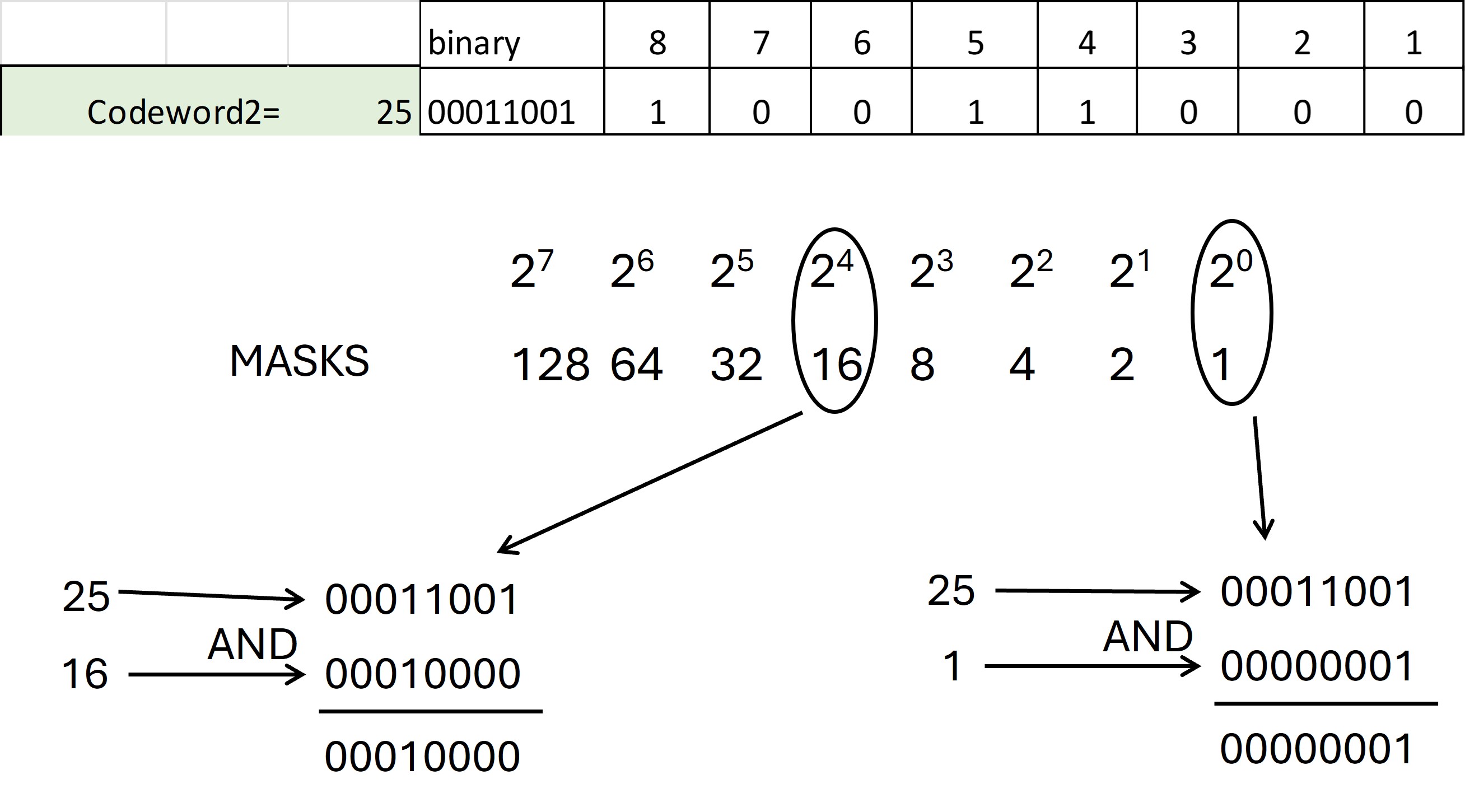
En la figura 25 se muestra como se realizarían las operaciones AND para cada bit de la clave 2 cuyo valor es 25 (00011001).
La estructura de la macro es como sigue:
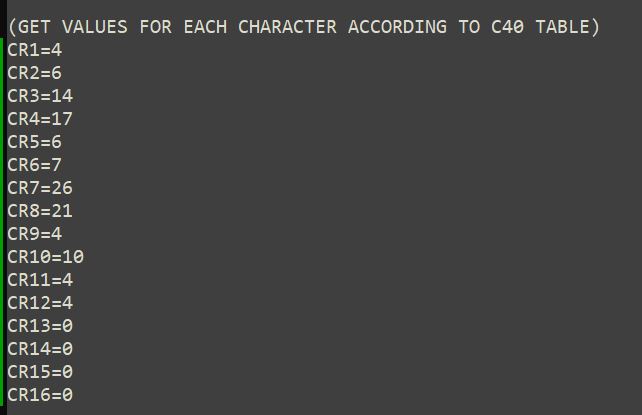
En la figura 26 se muestra como se declaran los valores en la macro de los caracteres de nuestro ejemplo de acuerdo a la tabla C40, en este caso se están declarando de manera directa.
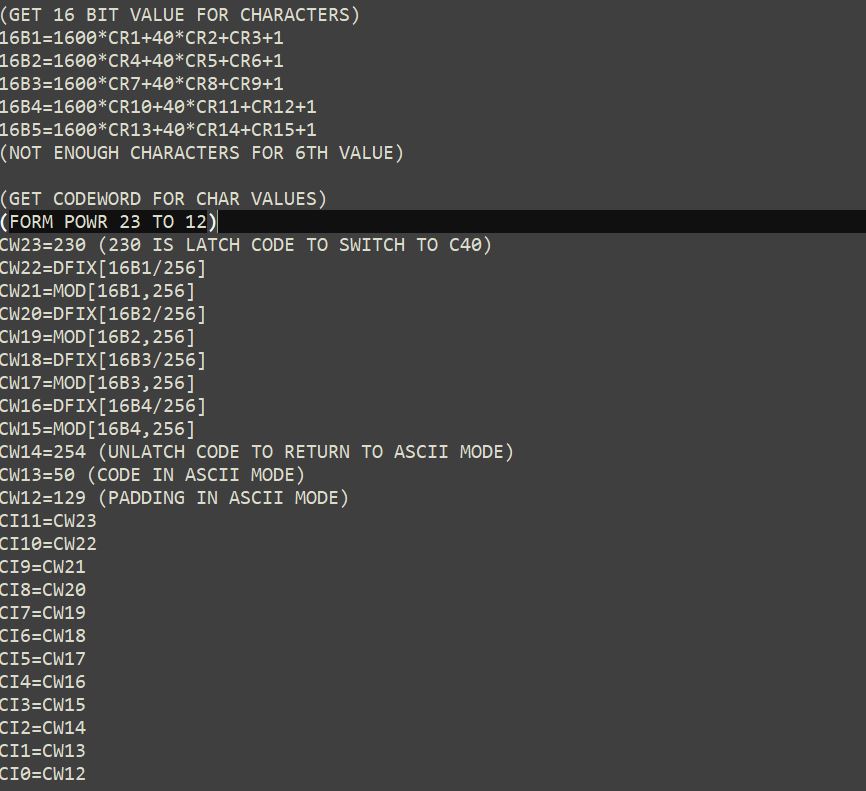
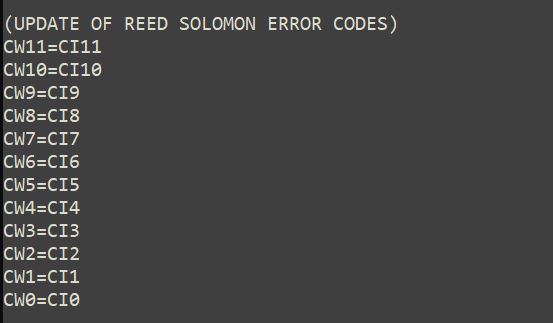
Los valores de 16 bits y las claves se calculan enseguida. Los valores de los coeficientes del dividendo se guardan en variables "temporales" CI. En este caso el símbolo puede acumular 12 claves de datos y 12 claves de corrección de error. Las claves de datos (12) se guardan en las variables CW23 a CW12 (el número corresponde a la potencia de la variable). Las variables CW0 a CW11 (las claves de corrección de error) se obtendrán de la división de polinomios.
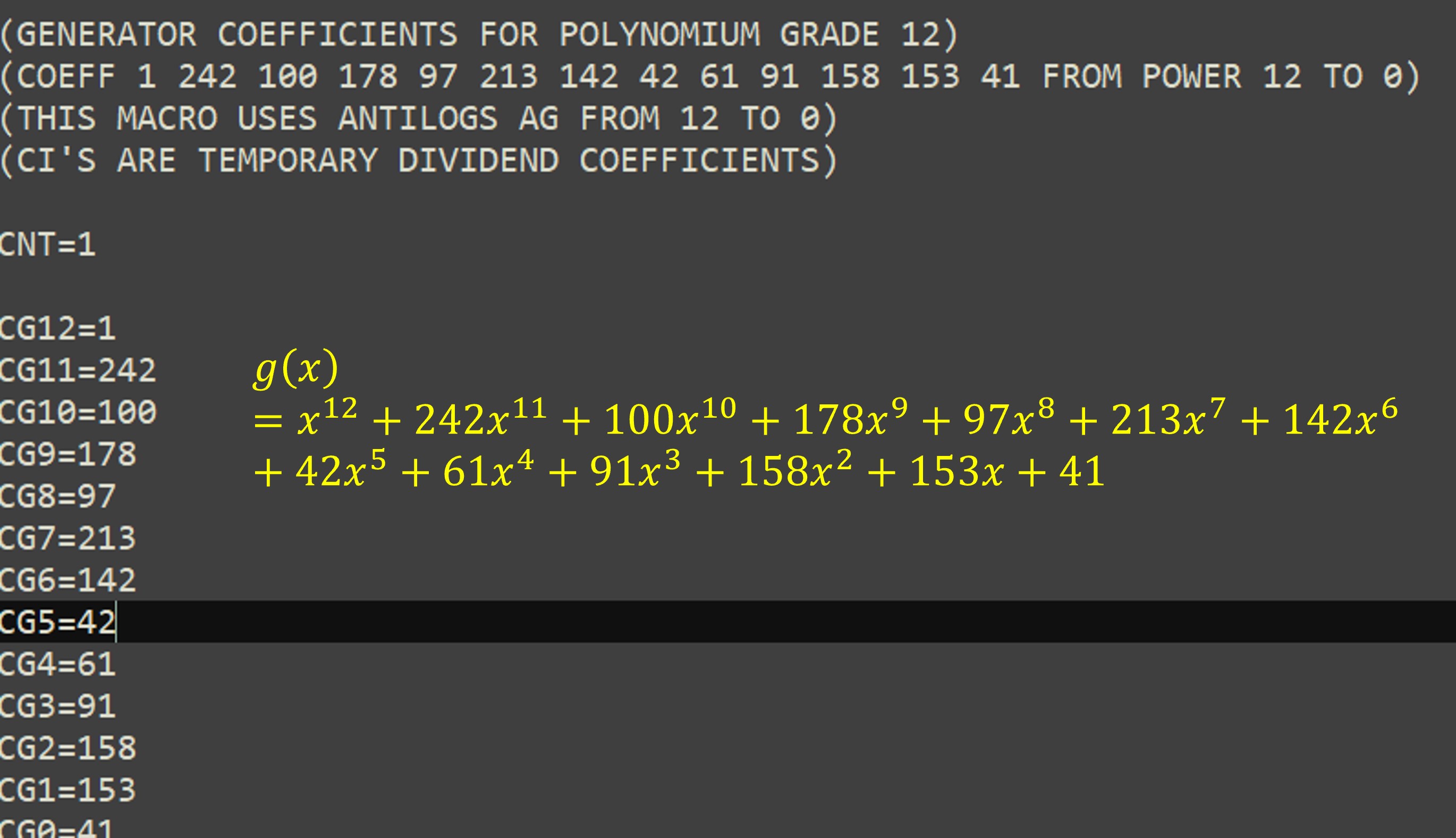
El valor del polinomio para la generar los códigos de error g(x) se tiene que declarar de forma directa (figura 28)
La realización de la división se realiza de forma iterativa usando las tablas de logaritmos y antilogaritmos. La operación requiere la operación XOR.
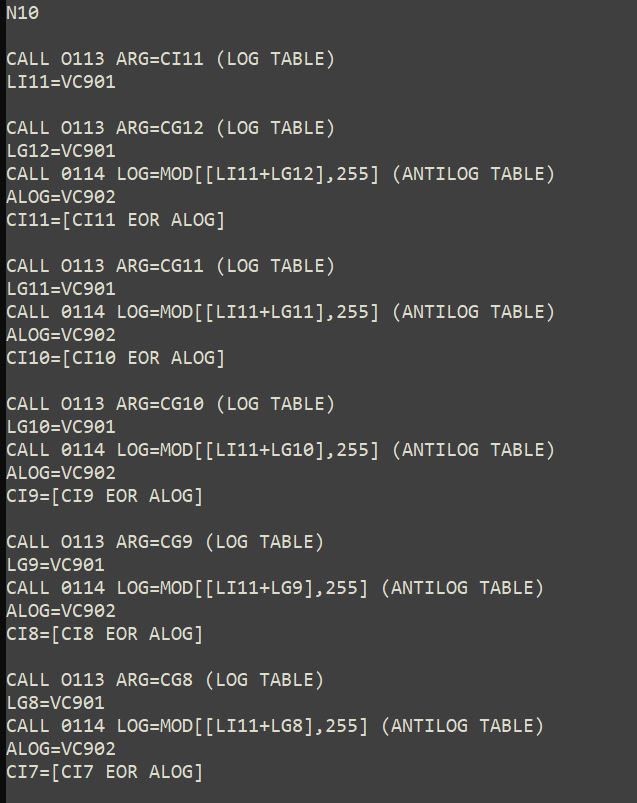
Los valores resultantes del residuo de la división actualizan las variables de corrección de error (figura 29)
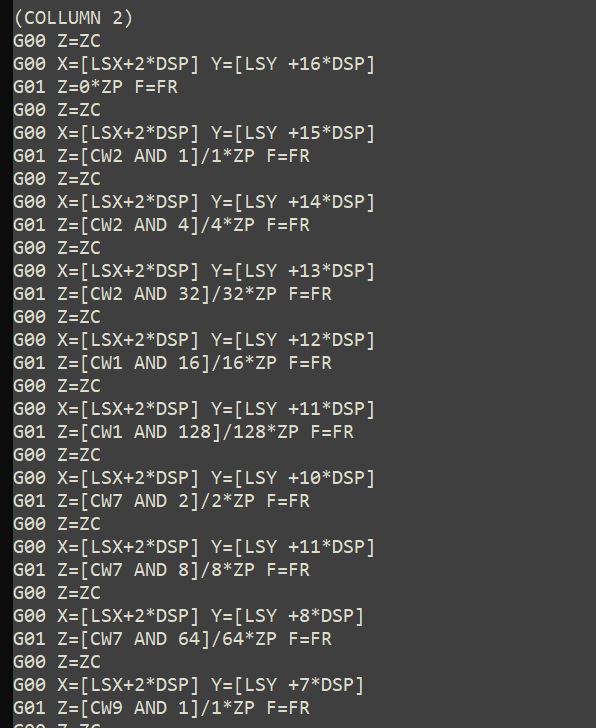
Por último se realiza el marcaje. El código para esta arreglado en columnas de manera que una operación AND determina si el bit correspondiente es 1 o 0.
Se puede lograr que la macro sea más sofisticada de manera que calcule automaticamente el tamaño del símbolo y las operaciones para el marcaje, pero el propósito era mantenerla lo más simple posible.